PhilosophyDay

Основные формы индуктивных рассуждений

Другая философия / Правдоподобные рассуждения / Основные формы индуктивных рассуждений

Страница 5

По-настоящему гипотетико-дедуктивные рассуждения начали применяться впервые в точном естествознании после того, как возник экспериментальный метод исследования и связанные с ним количественные методы.

О том, как применялся этот метод в конкретном исследовании, свидетельствуют "Беседы и математические доказательства ." Галилея. В них он подробно излагает способ аргументации, с помощью которого пришел к открытию и обоснованию своего важнейшего открытия – закона постоянства ускорения падающих тел. Сначала Галилей, как и его предшественники, придерживался гипотезы, что скорость падения тела (v) пропорциональна (к) пройденному пути (s), т.е. v = к s. Однако эксперимент не подтверждал ее, поэтому он принял другую гипотезу: скорость пропорциональна времени падения (t), т.е. v = g t, где g обозначает ускорение силы тяжести.

Из этой гипотезы чисто математически можно вывести заключение, что пройденный телом путь при падении пропорционален квадрату времени падения:

Наконец, из полученного заключения можно вывести бесчисленное множество частных следствий, если рассматривать пути, пройденные телом за 1, 2, 3 секунды:

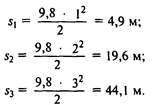
Во всех этих формулах s обозначает путь, t – время, g = 9,8 м/с2 – ускорение свободнопадающего тела.

Полученные результаты из исследования гипотезы можно проверить непосредственными измерениями, и тем самым подтвердить не только окончательное, но и промежуточные следствия из нее.

Построение своей теории Ньютон начинает с определения ее основных понятий и формулирования трех ее основных законов. Из них выводятся множество следствий, которые можно рассматривать как производные законы. В частности, из второго закона механики легко выводится закон свободного падения тел, открытый до этого Галилеем.

После Ньютона роль гипотетико-дедуктивного метода в построении и обосновании теорий опытных наук стала такой же общепризнанной, как и аксиоматического метода – для математических наук.